Временная сложность алгоритма
18 июля 2013
Временная сложность — это характеристика скорости работы алгоритма, оцениваемая по количеству элементарных операций (присвоение, сравнение, математические действия, битовые сдвиги, логические И, ИЛИ, НЕ), которые выполняет алгоритм при обработке входных данных размера n.
Из-за того, что значения входных данных могут меняться, то обычно подразумевается сложность для худшего случая, который обозначается как T(n). Например, при поиске числа в неотсортированном массиве из 1000 элементов, в лучшем случае алгоритму потребуется сделать одну операцию сравнения, если нужное число будет находиться в первом элементе массива. Но если нужное число будет находиться в последнем элементе или вообще не будет существовать в массиве, тогда алгоритму потребуется сделать 1000 сравнений, проверив каждый элемент массива.
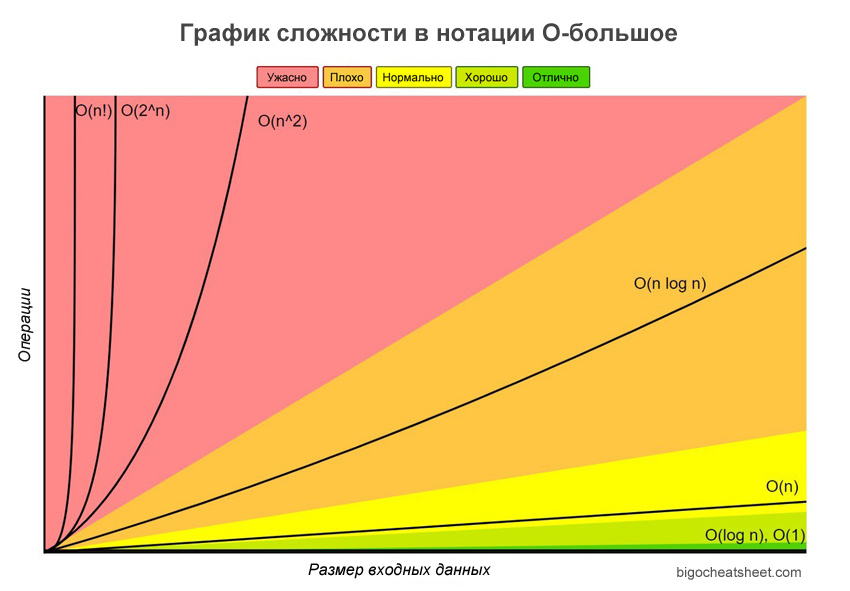
Сложность алгоритма описывается через O-нотацию, которая при подсчёте суммы элементарных операций учитывает только множитель или член самого высокого порядка и не учитывает постоянные коэффициенты.
Код на PHP:
Сложности активных строк:
1) 1
2) 1 + n
3) 1 + (n+1) + (n+n) = 1 + n + 1 + 2n
4) (1+1) * n = 2n
Итоговая сложность = 1 + 1 + n + 1 + n + 1 + 2n + 2n
В соответствии с О-нотацией опускаем постоянные коэффициенты (2) и получаем член с самым высоким порядком — n. Таким образом, функция будет иметь временную сложность O(n).
Из-за того, что значения входных данных могут меняться, то обычно подразумевается сложность для худшего случая, который обозначается как T(n). Например, при поиске числа в неотсортированном массиве из 1000 элементов, в лучшем случае алгоритму потребуется сделать одну операцию сравнения, если нужное число будет находиться в первом элементе массива. Но если нужное число будет находиться в последнем элементе или вообще не будет существовать в массиве, тогда алгоритму потребуется сделать 1000 сравнений, проверив каждый элемент массива.
Сложность алгоритма описывается через O-нотацию, которая при подсчёте суммы элементарных операций учитывает только множитель или член самого высокого порядка и не учитывает постоянные коэффициенты.
Пример подсчёта временной сложности алгоритма
Дана функция, которая находит сумму всех элементов массива.Код на PHP:
<?
/**
* Считает сумму всех элементов массива
* @param array $ar - массив
* @return int|float
*/
function sum_ar_elements($ar)
{
//СЛОЖНОСТЬ СТРОКИ = 1 присвоение
$r = 0;
//СЛОЖНОСТЬ СТРОКИ = 1 присвоение + n операций в функции count
$count = count($ar);
//СЛОЖНОСТЬ СТРОКИ = 1 присвоение $i + (n+1) операций сравнения + (n+n) операций сложения и присвоения в счётчике $i
for($i=0; $i<$count; $i++)
{
//СЛОЖНОСТЬ СТРОКИ = (1 присвоение + 1 сложение) * n повторений в цикле
$r = $r + $ar[$i];
}
return $r;
}
?>Сложности активных строк:
1) 1
2) 1 + n
3) 1 + (n+1) + (n+n) = 1 + n + 1 + 2n
4) (1+1) * n = 2n
Итоговая сложность = 1 + 1 + n + 1 + n + 1 + 2n + 2n
В соответствии с О-нотацией опускаем постоянные коэффициенты (2) и получаем член с самым высоким порядком — n. Таким образом, функция будет иметь временную сложность O(n).
Таблица некоторых временных сложностей
| Класс сложности | Сложность, T(n) | Пример алгоритма |
| Постоянная | O(1) | Сложение двух 16-битных чисел |
| Линейная | O(n) | Поиск наименьшего или наибольшего элемента в неотсортированном массиве |
| Квадратичная | O(n2) | Сортировка пузырьком, сортировка вставками |
| Кубическая | O(n3) | Классический алгоритм перемножения квадратных матриц размером n x n |
| Логарифмическая | O(log n) | Двоичный поиск |
| Линейно-логарифмическая | O(n log n) | Сортировка слиянием |
| Итерированно-логарифмическая | O(log* n) | Распределенная раскраска циклов |
| Экспоненциальная | O(2n), O(2^n) | Рекурсивное вычисление чисел Фибоначчи |
| Факториальная | O(n!) | Решение задачи коммивояжёра полным перебором (задача по поиску самого короткого маршрута между городами) |
